二叉树遍历终极总结版

二叉树遍历分为 前中后 遍历 + 层序遍历。

前序遍历

所谓前序遍历就是先遍历根节点，然后左儿子，然后右儿子。

前序遍历顺序为： A B D E C F G

中序遍历

所谓中序遍历就是先遍历左儿子，然后是根节点，然后是右儿子。

中序遍历顺序为：D B E A F C G

后序遍历

所谓后序遍历就是先遍历右儿子，然后是左儿子，然后是根节点。

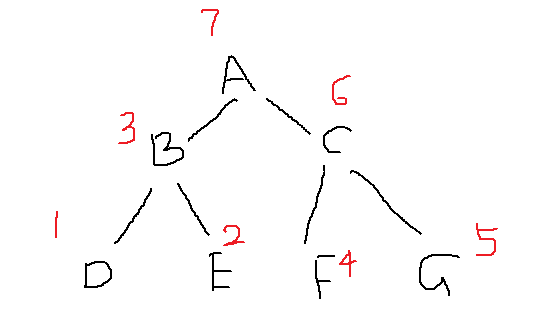
后序遍历顺序为：D E B F G C A

总结一下前中后，就是根节点在三个点中的位置。

层序遍历

层序遍历就是从上到下，从左到右顺序遍历树。

层序遍历的顺序：A B C D E F G

前中后遍历一般都是写一个深搜去递归。

前序遍历：

void dfs(TreeNode* root){
    //根节点
    if(root) res.push_back(root->val);
    //左儿子
    if(root->left) dfs(root->left);
    //右儿子
    if(root->right) dfs(root->right);
}

中序遍历：

void dfs(TreeNode* root){
    //左儿子
    if(root->left) dfs(root->left);
    //根节点
    if(root) res.push_back(root->val);
    //右儿子
    if(root->right) dfs(root->right);
}

后序遍历：

void dfs(TreeNode* root){
    //左儿子
    if(root->left) dfs(root->left);
    //右儿子
    if(root->right) dfs(root->right);
    //根节点
    if(root) res.push_back(root->val);
}

层序遍历：

层序遍历需要开辟一个队列来维护每一层的节点。

vector<vector<int>> levelOrder(TreeNode* root) {
    //bfs
    vector<vector<int>> res;
    queue<TreeNode*> q;
    if(root) q.push(root);
    //q中每次存的是一层
    while(q.size()){
        vector<int> level;
        int len=q.size();
        while(len--){
            auto t=q.front();
            q.pop();
            level.push_back(t->val);
            //这里维护的是下一层的节点
            if(t->left) q.push(t->left);
            if(t->right) q.push(t->right);
        }
        res.push_back(level);
    }
    return res;
}

另一种比较常见的题目就是给定两个遍历的方式，然后去寻找另一种遍历方式。
这里需要注意的是，给定的两个遍历方式中，必须有中序遍历。

比如给定了前序遍历和中序遍历，构建二叉树。

在前序遍历中，第一个点是根节点，而中序遍历中，根节点的左侧是左子树的成员，根节点的右侧是右子树的成员。所以只要找好中序遍历中的位置关系可以继续递归左子树和右子树。

在中序遍历中，左侧DBE是左子树的成员，右侧FCG是右子树的成员。
而在前序遍历中时限遍历根节点，然后是左子树然后是右子树，所以各类成员都是在一起的。
我们确定在中序遍历中，左子树成员的长度L，从前序遍历中，找到长度为L的为左子树的前序遍历，中序遍历中，右子树的长度为R，从前序遍历中，在左子树成员之后的为长度为R的为右子树的成员(这里只要找到起点就可以了，剩下的肯定是右子树成员)。

在编写代码之前先考虑一下，递归终止的条件。
如果前序遍历中没有元素了即终止。

代码:

unordered_map<int,int> pos;
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
    //二叉树的遍历 必须有中序遍历和其他两种遍历任意一个才能推出原二叉树
    //还是递归 先找到根节点
    //pos存的是中序遍历中点的下标
    for(int i=0;i<preorder.size();i++) pos[inorder[i]] = i;
    return build(preorder,inorder,0,preorder.size()-1,0,inorder.size()-1);
}

//函数返回的是树的根节点
TreeNode* build(vector<int> &preorder,vector<int> &inorder,int pl,int pr,int il,int ir){
    if(pl > pr) return NULL;
    auto root = new TreeNode(preorder[pl]);
    int k=pos[preorder[pl]];
    root->left = build(preorder , inorder , pl+1 , pl+k-il , il , k-1);
    root->right = build(preorder , inorder , pl+k-il+1 , pr , k+1 , ir);
    return root;
}

比如给定了后序遍历和中序遍历，构建二叉树。

后序遍历中最后一个点是根节点，中序遍历中根节点右侧为右子树，所以确定右子树成员FCG的长度，然后在后序遍历中FGC的长度确定了，则左子树就是最左侧到右子树上一个元素DEB。

代码：

unordered_map<int,int> pos;
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
    for(int i=0;i<inorder.size();i++) pos[inorder[i]] = i;
    return build(inorder,postorder,0,inorder.size()-1,0,postorder.size()-1);
}

TreeNode* build(vector<int> &inorder,vector<int> &postorder,int il,int ir,int pl,int pr){
    if(pl > pr) return NULL;
    auto root = new TreeNode(postorder[pr]);
    int k=pos[postorder[pr]];
    root->left = build(inorder,postorder , il , k-1 , pl , pl + k - 1 - il);
    root->right = build(inorder,postorder, k+1 , ir , pl + k -1 - il + 1 , pr-1);
    return root;
}

对中序遍历以及其它两种前序后序遍历总结：

函数返回的条件是前序或者后序的左右边界。
每次都是存储中序遍历中点的位置信息，然后寻找左子树和右子树的长度，然后递归。

比如给定了层序遍历和中序遍历，构建二叉树。

给定层序遍历，如果中序遍历中，根节点左右都有儿子且没有被使用过，则层序遍历的下一个点是根节点B的左儿子，再下一个点C是根节点的右儿子。

代码：

#include<iostream>
#include<string>
using namespace std;
string s1,s2;

void TarverseTree(int l1,int r1,int l2,int r2){
    //先找到层序遍历在中序遍历中的位置，每次递归的时候，层序遍历的第一个点是根节点
    int i,j;
    //层序遍历
    for(i = l2; i <= r2; i++){
        bool flag = false;
        //中序遍历
        for(j = l1; j <= r1; j++){
            if(s1[j] == s2[i]){
                cout<<s2[i];
                flag = true;
                break;
            }
        }
        if(flag) break;
    }
    
    if(j > l1) TarverseTree(l1, j - 1, l2, r2);
    if(j < r1) TarverseTree(j + 1, r1, l2, r2);
}
int main(){
    cin>>s1>>s2;
    
    TarverseTree(0, s1.size() - 1, 0, s2.size() - 1);
    return 0;
}

层序遍历与中序遍历组合总结：
函数每次处理的是中序遍历的边界，这一点与前序遍历 / 后序遍历 + 中序遍历不同。前者需要处理两个边界问题。

再有一类题目就是给定前序遍历找后序遍历，这种题目就不需要我们建树了，比如有如下的树。

前序遍历为： A B C
后序遍历为： B C A

如果给定的是前序遍历，只要在遍历的时候改变一下顺序，遍历完根节点之后，先遍历右子树，然后左子树。

得到如下： A C B
这时候只要将整个的顺序反转即可得到： B C A
即后序遍历。

如果给定后序遍历，只要在遍历的时候改变一下顺序，先遍历右子树，然后左子树，最后根节点。
得到如下： C B A
反转一下： A B C
即前序遍历。

二叉树遍历终极总结版

评论区