思路:

代码:
#include<iostream>
using namespace std;
const int N = 3010;
int n;
int a[N],b[N];
int f[N][N];
int main(){
cin>>n;
for(int i = 1; i <= n; i++) cin>>a[i];
for(int j = 1; j <= n; j++) cin>>b[j];
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
//不包含a[i]
f[i][j] = f[i - 1][j];
//包含a[i]
int maxv = 1;
if(a[i] == b[j]){
//统计包含的情况下的最大值 最后与不包含的比较
for(int k = 1; k < j; k++){
//maxv 统计1 ~ j - 1 中符合上升条件的 枚举 1 ~ j - 1中 只有前面的小于后面的才会去更新
if(b[k] < b[j]){
maxv = max(maxv,f[i - 1][k] + 1);
}
}
f[i][j] = max(f[i][j],maxv);
}
}
}
int res = 0;
for(int i = 1; i <= n; i++) res = max(res,f[n][i]);
cout<<res<<endl;
return 0;
}
上面的代码是三维的,我们在寻找1 ~ j - 1的过程中,对于每个j实际上都在重复的寻找,所以可以优化这一维。
下面这个条件进入的时候,是满足 a[i] == b[j]的所以,a[i] 可以换成b[j]
if(b[k] < b[j])
而k是从1递增到j的,遍历每个k的时候,只有满足 b[k] < b[j]才更新maxv,而b[j] == a[i],可以替换,所以是 b[k] < a[i],
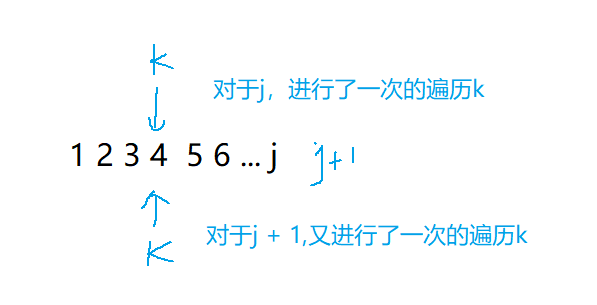
但是这样的工作是重复的,所以可以进行下面的优化:
for(int i = 1; i <= n; i++){
//maxv 用来维护选择a[i]的情况
int maxv = 1;
for(int j = 1; j <= n; j++){
//不包含a[i]
f[i][j] = f[i - 1][j];
//包含a[i] 以b[j]的上一个是什么来划分
if(a[i] == b[j]) f[i][j] = max(f[i][j],maxv);
//这里面的j实际上就是上面O(n^3)做法里面的k
if(b[j] < a[i]) maxv = max(maxv,f[i - 1][j] + 1);
}
}
最终优化的代码如下:
#include<iostream>
using namespace std;
const int N = 3010;
int n;
int a[N],b[N];
int f[N][N];
int main(){
cin>>n;
for(int i = 1; i <= n; i++) cin>>a[i];
for(int j = 1; j <= n; j++) cin>>b[j];
for(int i = 1; i <= n; i++){
int maxv = 1;
for(int j = 1; j <= n; j++){
//不包含a[i]
f[i][j] = f[i - 1][j];
//包含a[i] 以b[j]的上一个是什么来划分
//if(b[j] < a[i]) maxv = max(maxv,f[i - 1][j] + 1);
if(a[i] == b[j]) f[i][j] = max(f[i][j],maxv);
if(b[j] < a[i]) maxv = max(maxv,f[i - 1][j] + 1);
}
}
int res = 0;
for(int i = 1; i <= n; i++) res = max(res,f[n][i]);
cout<<res<<endl;
return 0;
}

评论区