LeetCode 174. 地下城游戏

LeetCode 174. 地下城游戏

思路：
状态表示为 该点到终点 f[n - 1][m - 1]的最小初始血量，我们求出每个点到终点的最小最初血量，则f[0][0]就是答案。
看一下一般的情况，如下图。

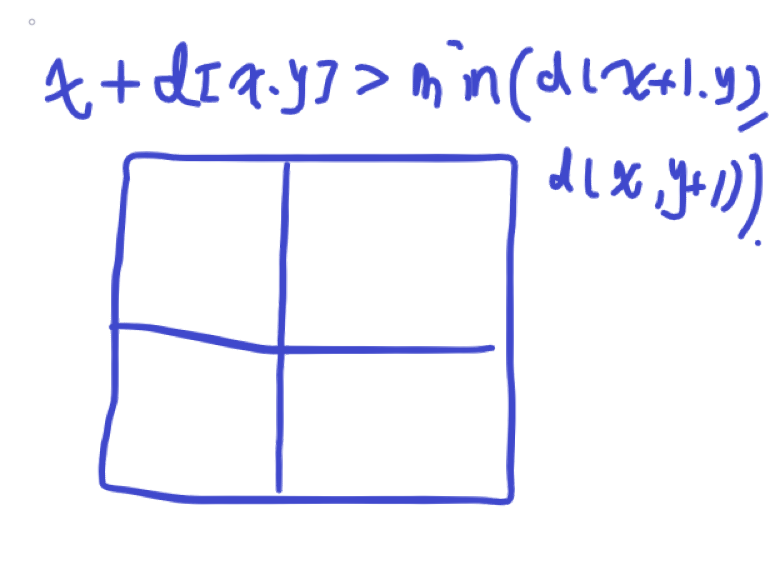
设左上角的最小最初血量为x，则点(x,y)可以移动到右侧或下侧，所以x + d[x,y] > min(d[x + 1][y],d[x][y + 1])即可，因为我们求的是最小而不是两边兼顾。

代码：

class Solution {
public:
    int calculateMinimumHP(vector<vector<int>>& dungeon) {
        int n = dungeon.size();
        int m = dungeon[0].size();
        vector<vector<int>> f(n + 1,vector<int> (m + 1, 1e8));
        for(int i = n - 1;i >= 0;i--){
            for(int j = m - 1; j >= 0 ;j--){
                if(i == n-1 && j == m - 1) f[i][j] = max(1,1 - dungeon[i][j]);
                else{
                    if(i + 1 < n) f[i][j] = f[i + 1][j] - dungeon[i][j];
                    if(j + 1 < m) f[i][j] = min(f[i][j],f[i][j + 1] - dungeon[i][j]);
                    f[i][j] = max(1 , f[i][j]);
                } 
            }
        }
        return f[0][0];

    }
};